C++实验八:魔方问题
首先现在看到题目的我一脸懵。
魔方问题:
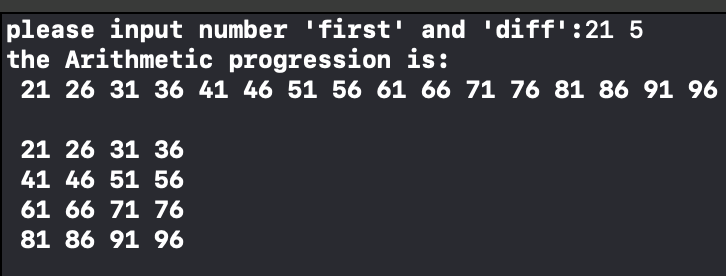
- 编写函数createArithmeticSeq(),提示用户输入两个数字first和diff。然后函数创建一个按算术顺序排列的、有16个元素的数组并输出该算术序列。例如,如果first=21,diff=5,那么算术序列是21 26 31 36 41 ……96。
- 编写函数matricize(),它将一个有16个元素的一维数组和一个4行4列的二维数组作为参数。(其它的值,例如数组的大小,也必须作为参数来传递。)该函数将一维数组的元素放入到二维数组中。例如,如果A是在a中创建的一维数组,B是二维数组,那么将A的元素放入到B中后,数组B是:
21 26 31 36
41 46 51 56
61 66 71 76
81 86 91 96
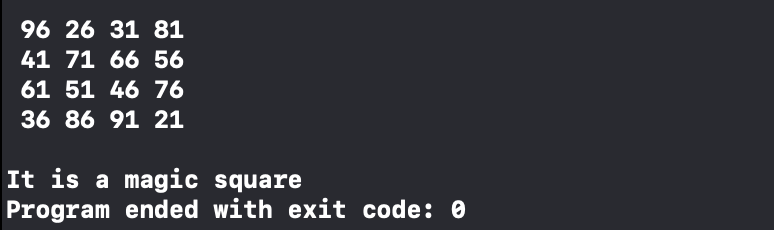
- 编写一个函数reverseDiagonal(),倒转二维数组的两个对角线。例如,如果二维数组如b所示,那么在倒转两个对角线后,二维数组是:
96 26 31 81
41 71 66 56
61 51 46 76
36 86 91 21
- 编写一个函数magicCheck(),它将一个有16个元素的一维数组、一个4行4列的二维数组以及数组的大小作为参数。通过将一维数组的所有元素相加后被4除,该函数得到了magicNumber。该函数然后将每一行、每一列以及两个对角线的元素相加,然后将每一次的和与magicNumber相比较。如果每一行、每一列以及两个对角线的元素和等于magicNumber,那么函数输出“It is a magic square”,否则输出“It is not a magic square”。不必打印每一行、每一列以及每个对角线的元素和。
- 编写一个函数printMatrix(),输出二维数组的元素,每行显示数组的一行。输出应该尽可能接近正方形的形式。
- a到e编写的函数处理元素时应用循环来完成。可以根据需要自行设计函数实现一些子功能,比如实现对角线相加的函数,实现行列相加的函数。
- 使用下面的main()函数来测试从a到e编写的程序。
const int rows = 4;
const int columns = 4;
const int listSize = 16;
int main()
{
int list[listSize];
int matrix[rows][columns];
createArithmeticSeq(list,listSize);
matricize(list, matrix, rows);
printMatrix(matrix, rows);
reverseDiagonal(matrix, rows);
printMatrix(matrix, rows);
magicCheck(list, matrix, listSize, rows);
return 0;
}
不管了,先借鉴一波······百度文库
我将C简单修改后成为合格的C++程序,编译通过。
#include
using namespace std;
const int rows = 4;
const int columns = 4;
const int listSize = 16;
int main()
{
int list[listSize]={0};
int matrix[rows][columns];
void createArithmeticSeq(int list[listSize], int listSize);
void matricize(int list[listSize],int matrix[rows][columns], int rows);
void printMatrix(int matrix[rows][columns], int rows);
void reverseDiagonal(int matrix[rows][rows],int rows);
void magicCheck(int list[listSize],int matrix[rows][columns], int listSize,int rows);
createArithmeticSeq(list,listSize);
matricize(list,matrix,rows);
printMatrix(matrix,rows);
reverseDiagonal(matrix,rows);
printMatrix(matrix, rows);
magicCheck(list,matrix,listSize,rows);
}
void createArithmeticSeq(int list[listSize], int listSize)
{
int i;
int a,b;
cout<<"please input number 'first' and 'diff':"; cin>>a >>b;
list[0]=a;
for(i=1;i<listSize;i++)
list[i]=list[i-1]+b;
cout<<"the Arithmetic progression is:\n";
for(i=0;i<listSize;i++)
cout<<" "<<list[i];
cout<<"\n";
cout<<"\n";
}
void matricize(int list[listSize], int matrix[rows][columns],int rows)
{
int i,j;
for(i=0;i<rows;i++)
for(j=0;j<rows;j++)
matrix[i][j]=list[rows*i+j];
}
void printMatrix(int matrix[rows][columns], int rows)
{
int i,j;
for(i=0;i<rows;i++)
{
{ for(j=0;j<rows;j++)
cout<<" "<<matrix[i][j];
}
cout<<"\n";
}
cout<<"\n";
}
void reverseDiagonal(int matrix[rows][columns], int rows)
{
int i,j,t,k;
for(i=0;i<2;i++)
for(j=0;j<rows;j++)
{
if(i==j)
{
t=matrix[i][j];
matrix[i][j]=matrix[3-i][3-j];
matrix[3-i][3-j]=t;
}
if(i+j==3)
{
k=matrix[i][j];
matrix[i][j]=matrix[j][i];
matrix[j][i]=k;
}
}
}
void magicCheck(int list[listSize], int matrix[rows][columns], int listSize,int rows)
{
int i,j,c,m=0,n=0;
for(i=0;i<listSize;i++)
m+=list[i];
c=m/rows;
m=0;
for(i=0;i<rows;i++)
{
for(j=0;j<rows;j++)
{
m+=matrix[i][j];
}
if(m!=c)
{
cout<<"It is not a magic number\n";
return ;
}
m=0;
}
for(i=0;i<rows;i++)
{
for(j=0;j<rows;j++)
{
m+=matrix[j][i];
}
if(m!=c)
{
cout<<"It is not a magic number\n";
return ;
}
m=0;
}
for(i=0;i<rows;i++)
{
for(j=0;j<rows;j++)
{
if(i==j)
m+=matrix[i][j];
if(i+j==3)
n+=matrix[i][j];
}
}
if(m!=c)
{
cout<<"It is not a magic number\n";
return ;
}
if(n!=c)
{
cout<<"It is not a magic number\n";
return ;
}
cout<<"It is a magic square\n";
}
于是乎就这样吧!
运行结果:
1.腾龙梦屋文章内容无特殊注明皆为源儿原创,转载请注明来源,谢谢!
2.若有相关文章侵犯您的权益,请联系源儿删除,谢谢!
3.相关软件、资料仅供学习参考使用,在24h内务必删除!
腾龙梦屋 » C++实验八:魔方问题
2.若有相关文章侵犯您的权益,请联系源儿删除,谢谢!
3.相关软件、资料仅供学习参考使用,在24h内务必删除!
腾龙梦屋 » C++实验八:魔方问题






 加速支持
加速支持