数据结构实验五:树

实验五 树的基本操作

一、实验目的

1、进一步掌握指针变量、动态变量的含义。

2、掌握二叉树的结构特性，以及各种存储结构的特点和适用范围。

3、掌握用指针类型描述、访问和处理二叉树的运算。

二、实验内容

1、设计和编写程序，按照输入的遍历要求（即先序、中序和后序）完成对二叉树的遍历，并输出相应遍历条件下的树结点序列。

2、设计和编写程序，输出所有从根到叶子的路径。

3、赫夫曼树的算法。（可选作）

报告内容为小组共同完成

一、实验目的
1、进一步掌握指针变量、动态变量的含义。
2、掌握二叉树的结构特性，以及各种存储结构的特点和适用范围。掌握用指针类型描述、访问和处理二叉树的运算。
3、掌握用指针类型描述、访问和处理二叉树的运算法。
二、实验内容
1、设计和编写程序，按照输入的遍历要求（即先序、中序和后序）完成对二叉树的遍历，并输出相应遍历条件下的树结点序列。
2、设计和编写程序，输出所有从根到叶子的路径。
三、代码实现

#include<iostream>
#define MAXSIZE 100
using namespace std;
//二叉树数据结构定义
typedef struct BiTreeNode
{
    char data;                //结点数据域
    struct BiTreeNode* lchild;    //左孩子指针
    struct BiTreeNode* rchild;    //右孩子指针
}BiTreeNode, * BiTree;

//二叉树按照先序方式建立
void CreateBiTree(BiTree& T)
{
    char a;
    cin >> a;
    if (a == '0')
        T = NULL;         //表示为空枝
    else
    {
        T = new BiTreeNode[MAXSIZE];  //根节点
        T->data = a;                
        CreateBiTree(T->lchild);    //创建左子树
        CreateBiTree(T->rchild);    //创建右子树
    }
}

//先序遍历   
void PreOrderTravel(BiTree T)
{
    if (T == NULL)
        return;
    cout << T->data << " ";                
    PreOrderTravel(T->lchild);          
    PreOrderTravel(T->rchild);          
}

//中序遍历 
void InOrderTravel(BiTree T)
{
    if (T == NULL)
        return;
    InOrderTravel(T->lchild);
    cout << T->data << " ";
    InOrderTravel(T->rchild);
}

//后序遍历 
void TailOrderTravel(BiTree T)
{
    if (T == NULL)
        return;
    TailOrderTravel(T->lchild);
    TailOrderTravel(T->rchild);
    cout << T->data << " ";
}


char path[MAXSIZE];
int pathlen = 0;

void FindPath(BiTree& T)
{
    if (T != NULL)
    {
        if (T->lchild == NULL && T->rchild == NULL)    //左子树与右子树为空，指这个树一个路径停止
        {
            path[pathlen++] = T->data;                //将这条路径的所有数据保存到数组中
            for (int i = 0; i < pathlen; i++)
            {
                cout << path[i];            //展示路径
            }
            cout << endl;
            pathlen--;
            return;
        }
        else                                      //当路径没有到终点时，对每一条路径的数据进行访问
        {
            //采用先序遍历的方法进行访问
            path[pathlen++] = T->data;     //保存数据
            FindPath(T->lchild);     //查找左子树数据
            FindPath(T->rchild);     //查找右子树数据
            pathlen--;               //返回到上一级，进行下一次的下一个路径的访问
        }
    }
}

int main()
{
    BiTree T;
    T = new BiTreeNode[MAXSIZE];
    cout << "请按照先序方式依次输入每一个结点的值（空结点请输入 0）:"<< endl;
    CreateBiTree(T);
    cout << "先序方式遍历二叉树的结果为：";
    PreOrderTravel(T);
    cout << endl;
    cout << "中序方式遍历二叉树的结果为：";
    InOrderTravel(T);
    cout << endl;
    cout << "后序方式遍历二叉树的结果为：";
    TailOrderTravel(T);
    cout << endl;
    cout << "二叉树中从根到叶子结点的所有路径如下：" << endl;
    FindPath(T);
    return 0;
}

四、实验难点
1、对递归过程的理解
做实验的时候组内有同学说没想到做个遍历问题没想到还要用到栈，其实这个并不奇怪，因为递归的过程本质上也就是在对栈空间的使用。
如果你调用了一个函数，编译器会把这个函数（以某种标志比如说地址）压入栈中，当你在一个函数中调用自己或别的函数（这里是自己调用自己）的时候，编译器先停止执行当前函数正在执行的内容，并在栈中该函数所处位置记录当前函数执行到的位置（也是地址）。而当一个函数执行结束后会从栈中弹出，继续执行栈顶未执行完的内容。如果还有调用函数则一直执行上述内容直至栈空。
这也告诉我们一点，就是递归的使用是必须有截止条件的，如果没有截止条件，就会无限制地递归下去，直到栈空间溢出。
2、对二叉树三种遍历方式的理解以及实现
其实无论是先序遍历的根左右，中序遍历的左根右以及后序遍历的左右根，这里的根指的是根节点，左指的是左子树，右指的是右子树，都只需要记住的是一点，我们遍历的是子树（叶子节点也算）。这样我们就可以根据我们遍历的原则去遍历相应的子树。以中序遍历为例，我们对任意一棵子树都是先去遍历其左子树，然后在遍历完左子树后访问根节点，然后再完遍历其右子树。遍历到最后一定是叶子节点，对于叶子节点这种子树，无论是什么遍历都只用访问它自己（其实图画的挺清楚了）。
递归过程其实图也画得挺清楚了。

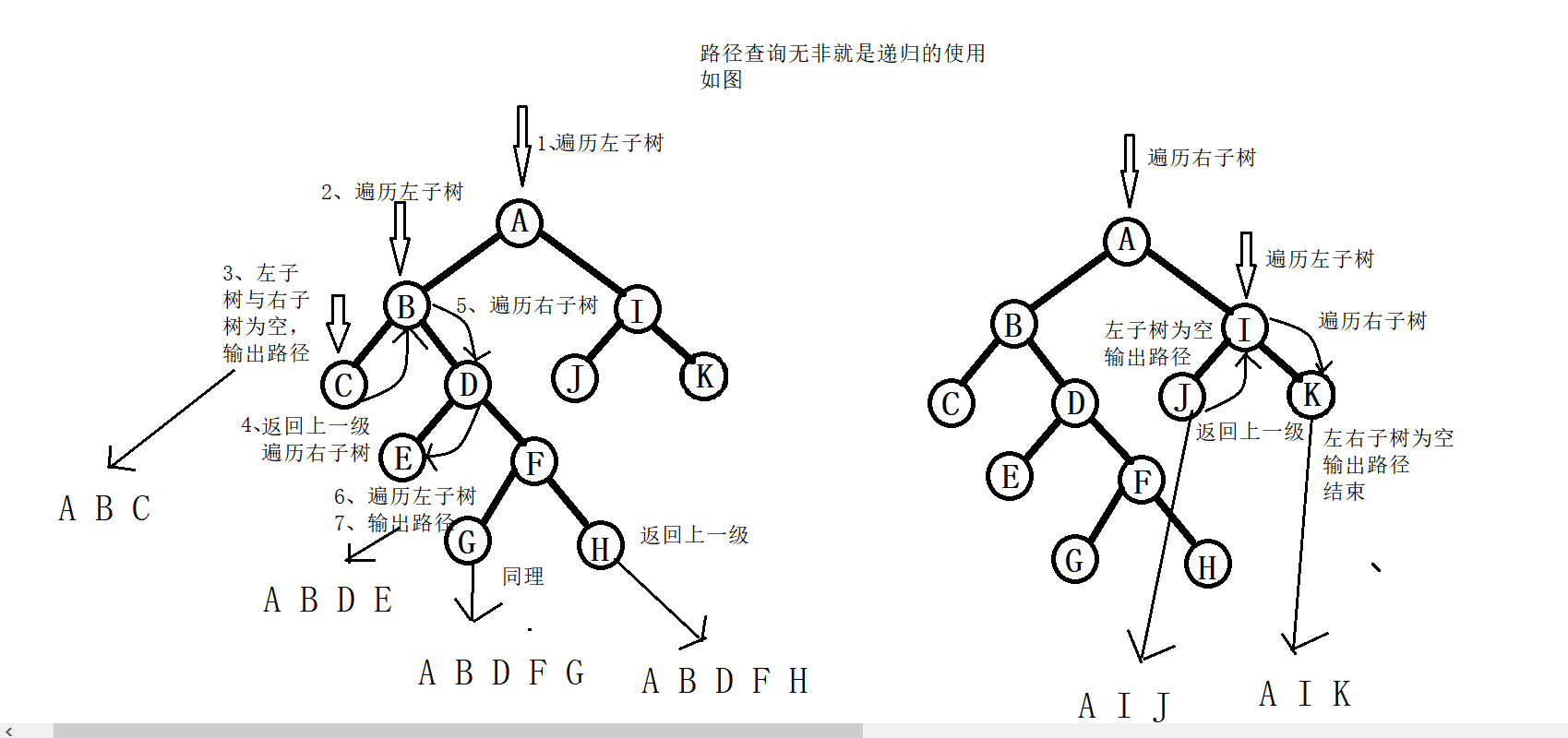
五、实验心得
在本次实验中，在求解树的遍历问题以及求根到所有叶子节点的路径问题时，都使用了递归的做法。递归的做法好处挺明显的，就是代码量短，逻辑结构比较清晰，比较易于编写。而其带来的缺点则是对于一个问题有可能带来冗余的递归（原来就递归出答案了，但是因为问题的性质还是要再往那个方向递归），这样有可能会带来许多不必要的时间开销，甚至会让时间复杂度增长非常快。对于这样的情况，有一种解决的办法就是记忆化，即将已经搜过的点也好，值也好，记录下来，这样在再次访问时就可以避免不必要的多余访问，一个很直白的例子就是深度优先搜索中为了防止重复遍历而设计的visited标记。
其实从解决这节实验课的问题我们也可以发现，递归是一种非常实用的方法，深入理解，合理使用，递归会成为我们解决问题，编写代码的利器。